03b - MATLAB basics

03b - MATLAB basics

What’s MATLAB?

MATLAB is an integrated environment for mathematical and engineering calculation, simulation and scripting. The name comes from MATrix LABoratory. Nowadays its capabilities run far beyond matrix operations, and the program is used in many fields. Besides base calculation core, many specialized libraries called toolboxes are available. Among MATLAB alternatives, open source GNU Octave software project can be distinguished, which aims for best compatibility with MATLAB language.

Because MATLAB’s main focus were interactive calculations, its language is designed as an interpreted language, in contrast to compiled languages such as C or C++.

πŸ”¨ πŸ”₯ Assignment πŸ”₯ πŸ”¨

Run the MATLAB environment.

MATLAB interface and GNU Octave GUI

Main window of MATLAB environment is shown below:

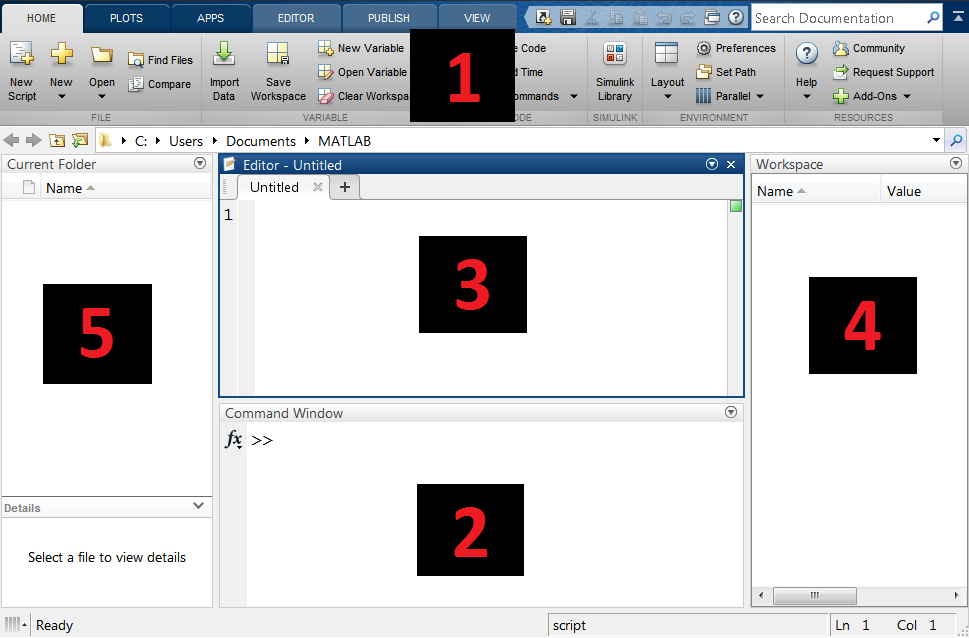
Matlab_Okno1

All tools are grouped in ribbons, located at the top of the window (1). Command line (2) located at the bottom can be used for interactive calculation by manual command input. More elaborate computation can be done using script files, edited in the central part of the window (3). Workspace with current variables is located on the right (4), and current directory contents are shown on the left (5).

Default layout can always be restored using Layout β†’ Default command, located in Home ribbon:

Matlab_Okno2

Main window of GNU Octave GUI has a similar layout:

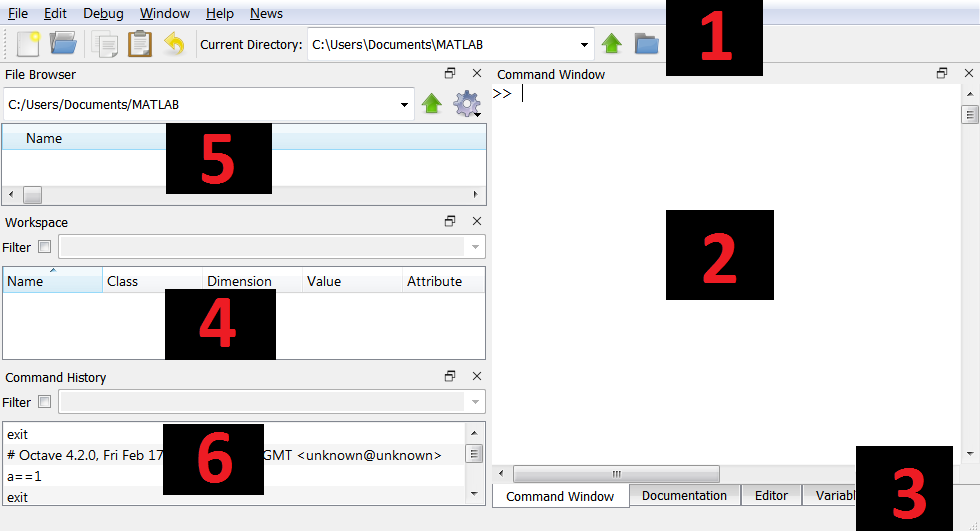
Octave_Okno1

Basic tools are available at the top (1). Command line (2) is located on the right, but can be switched to script editor osing tabs at the bottom (3). On the right, there is a column with three elements, from the top: current directory file browser (5), workspace variables (4) and command history (6).

If layout has been changed, it can always be restored using Window β†’ Reset Default Window Layout:

Octave_Okno2

MATLAB basics

Basic mathematical operations

In MATLAB, you can use basic mathematical operators, such as +, -, *, /, keeping order of operations. To force different order, () parentheses can be used:

>> 3 + 5

ans =
     8

>> 9 - 8 * 100

ans =
  -791

>> (9 - 8) * 100

ans =
   100

>> 100 / 6

ans =
   16.6667

Exponentiation can be done using caret operator ^:

>> 2 ^ 16

ans =
       65536

πŸ”¨ πŸ”₯ Assignment πŸ”₯ πŸ”¨

  1. Test all of above operators in MATLAB command line.

  2. A rocket accelerates uniformly with acceleration of 100 m/s^2. Calculate the distance it will travel in 10 seconds. Hint: acceleration

All entered commands are saved in history, which can be accessed using up/down arrows on the keyboard. In MATLAB, this causes a history pop-up to appear, in Octave it is always visible on the left. Commands accessed from history can be edited.

πŸ”¨ πŸ”₯ Assignment πŸ”₯ πŸ”¨

Check how history works in MATLAB.

Variables

MATLAB language allows for storing values in variables. Assignment to a variable can be done using = operator. Variable type is chosen automatically based on assigned contents:

>> base = 20

base =
    20

>> height = 3

height =
     3

>> base * height / 2

ans =
    30

Computed results can be saved to a variable:

>> netto = 100

netto =
   100

>> tax = 1.23

tax =
    1.2300

>> brutto = netto * tax

brutto =
   123

String literals are enclosed in single quotes '. If a single quote has to be present in the string itself, it has to be prepended with another one:

>> s1 = 'Anna has a dog'

s1 =
    'Anna has a dog'

>> s2 = 'This is Anna''s dog'

s2 =

    'This is Anna's dog'

πŸ”¨ πŸ”₯ Assignment πŸ”₯ πŸ”¨

  1. Using command line, assign length of a square diagonal to d variable.
  2. Based on d, calculate length of square side and save in variable a. Hint diagonal, remember that calculating square root of a number is the same as raising a number to the power of 0.5.
  3. Using the result, calculate area of a circle inscribed in the square. Hint Ο€ value can be accessed using pi command.

Vector and matrix operations

Vectors

In MATLAB, a vector can be defined by providing a space-separated list of values enclosed in square brackets []:

>> primes = [2 3 5 7 11 13 17 19 23 29 31 37]

To access vector elements, round parentheses () operator can be used. Single elements or ranges can be accessed. Remeber that in contrast to most programming languages, array indexes in MATLAB start at 1:

>> primes(1)

ans =
     2

>> primes(2:5) % right-closed (inclusive) interval

ans =
     3     5     7    11

>> primes(3:end) % interval from 3 to vector end

ans =
     5     7    11    13    17    19    23    29    31    37


>> primes(1:2:end) % every other element

ans =
     2     5    11    17    23    31

Separating values with semicolons ; causes them to be placed in rows, creating a column vector:

>> a = [1; 2; 3; 4]

a =
     1
     2
     3
     4

A signle quote ' can be used to transpose the vector, giving the same effect:

>> a = [1 2 3 4]

a =
     1     2     3     4

>> a'

ans =
     1
     2
     3
     4

Vectors can be concatenated using square brackets []:

>> a = [1 2]

a =
     1     2

>> b = [3 4]

b =
     3     4

>> [a b]

ans =
     1     2     3     4

Vectors can also be created using a : range operator:

>> x = [1:10]

x =
     1     2     3     4     5     6     7     8     9    10

It is also possible to specify step different than 1:

>> t = [0:0.01:1] % creates a vector from 0 to 1 (inclusive)
                  % with 0.01 step (which results in a 101-element vector)

>> z = [10:2:20]  % creates a vector from 10 to 20 (inclusive)

Vectors of compatible sizes can be added and subtracted (+, -):

>> a = [1 2 3 4 5]

a =
     1     2     3     4     5

>> b = [6 7 8 9 10]

b =
     6     7     8     9    10

>> a + b

ans =
     7     9    11    13    15

>> a - b

ans =
    -5    -5    -5    -5    -5

Multiplication on vectors/matrices using * operator is done as a matrix operations. By multiplying a row vector by a column vector, a vector dot product is achieved:

>> a * b'

ans =
   130

Element-wise multiplication can be done using a .* operator:

>> a .* b

ans =
     6    14    24    36    50

Length of a vector can be accessed using length() function:

>> length(a)

ans =
     5

Matrices

In MATLAB matrices are defined similarly to vectors, with each row separated with semicolons (;):

>> y = [1 2 3; 4 5 6; 7 8 9]

y =
     1     2     3
     4     5     6
     7     8     9

Again, elements can be accessed using parentheses operator (), by providing a pair of indexes. The first parameter specifies row(s), the second specifies column(s). Indexing starts at 1:

>> y(1,3)

ans =
     3

>> y(1:2,1:2)

ans =
     1     2
     4     5

Similarly to vectors, basic math operations are supported: +, -, *, .*, /, ./. A matrix can be transposed using a single quote operator '. Remeber that in matrix multiplication, order of arguments matters!

>> y * y'

ans =
    14    32    50
    32    77   122
    50   122   194

>> y' * y

ans =
    66    78    90
    78    93   108
    90   108   126

Vectors and matrices can also be used in math operations with scalars:

>> y * 3

ans =
     3     6     9
    12    15    18
    21    24    27

>> y + 3

ans =
     4     5     6
     7     8     9
    10    11    12

Matrix size can be accesed using size() function. The function returns a two-element vector containing number of rows and columns:

>> c = [1 2 3; 4 5 6]

c =
     1     2     3
     4     5     6

>> size(c)

ans =
     2     3

πŸ”¨ πŸ”₯ Assignment πŸ”₯ πŸ”¨

  1. Create 3 vertical vectors of length 5, filled with various values. Concatenate them horizontally to create a 5x3 matrix.
  2. Multiply the resulting matrix by the same matrix, transposed.
  3. Myltiply the result by 10.

Creating basic matrices

Apart from providing values manually, some matrices can be obtained using dedicated functions. Their arguments are usually matrix dimensions: number of rows and number of columns. Supplying a single argument will result in a single n x n matrix.

>> zeros(3,3) % matrix filled with zeros

ans =
     0     0     0
     0     0     0
     0     0     0

>> ones(2,5) % matrix filled with ones

ans =
     1     1     1     1     1
     1     1     1     1     1

>> eye(4) % identity matrix

ans =
     1     0     0     0
     0     1     0     0
     0     0     1     0
     0     0     0     1

>> rand(2,2) % random values from range <0, 1>

ans =
    0.8147    0.1270
    0.9058    0.9134

πŸ”¨ πŸ”₯ Assignment πŸ”₯ πŸ”¨

Using above functions create a 4 x 6 (rows x columns) matrix filled with value 5.

Math funcitons

MATLAB has a wide range of mathematical functions built-in, below is a very small excerpt of them:

Function Description
sin(a) trigonometric functions, arguments in radians
cos(a)
tan(a)
cot(a)
sind(a) trigonometric functions, arguments in degrees
cosd(a)
tand(a)
cotd(a)
sqrt(a) square root
exp(a) natural exponential function (e^a)
log(a) natural logarithm
log10(a) base-10 logarithm
abs(a) absolute value

Examples:

>> sin(pi/2)

ans =
     1

>> sin([0:5])

ans =
     0    0.8415    0.9093    0.1411   -0.7568   -0.9589

πŸ”¨ πŸ”₯ Assignment πŸ”₯ πŸ”¨

  1. Create a vector containing integers from -10 to 10.
  2. Using known functions, create a vector of absolute values of above vector.
  3. Calculate square root values of above vector.

Executable scrips

During normal MATLAB operation, the commands are rarely input directly in the command line, but rather executed from a text file - a script. Scripts in MATLAB have a .m file extension. A new script can be created using New Script in HOME ribbon. A new script Editor window will be opened. The script can be saved by clicking on Save command in EDITOR ribbon. When choosing a script filename, use only alpahnumeric characters and underscore (_).

πŸ”¨ πŸ”₯ Assignment πŸ”₯ πŸ”¨

  1. Create a new script.
  2. Save it as my_first_script.m.

To run a script, click RUN in EDITOR ribbon. Alternatively, press F5 on the keyboard. The script results will be shown in the console.

πŸ”¨ πŸ”₯ Assignment πŸ”₯ πŸ”¨

  1. Add simple code to the newly created script, for example:
a = 1
b = 4

a * b
  1. Run the script.

By default, MATLAB displays the result of each operation in console. The output can (and usually should) be silenced by adding a semicolon (;) at the end of each command.

πŸ”¨ πŸ”₯ Assignment πŸ”₯ πŸ”¨

  1. Modify the script so that assignment to variables is not displayed in the console.
  2. Run the script.

Each script can also be run directly from the command line, by inputting the script name as a command. Similiarly, they can be run from another script.

πŸ”¨ πŸ”₯ Assignment πŸ”₯ πŸ”¨

Run your script from the command line.

Plots

MATLAB provides an easy to use plotting interface. To display a simple 2D plot, a plot(x,y) can be used, by providing two vectors of corresponding XY values. By default the points are connected with straight lines.

πŸ”¨ πŸ”₯ Assignment πŸ”₯ πŸ”¨

  1. Copy the code below to your script and execute:
x = [1 2 3 4];
y = [1 2 3 4];

plot(x,y,'-o')

grid on
  1. Change y values to [1 2 1 2]. Run the script and see the result.
  2. Change x values to [1 2 2 1]. Run the script. As you can see, the input points don’t have to represent a function.

An optional third argument can be provided to change the plot’s appearance. It can modify line color and style or specify markers placed in each point. Detailed help of each MATLAB function can be obtained using a doc function command, for example:

doc plot

πŸ”¨ πŸ”₯ Assignment πŸ”₯ πŸ”¨

  1. Using command line, open plot function documentation.
  2. Go to section Input Arguments -> Line Spec.
  3. Modify the script so that the plot is displayed with a dashed red line, and points are marked with cross symbols.

Subsequent plot calls overwrite current figure contents. This behavior can be changes using below command:

hold on

After calling hold on, each subsequent plot call will append data to the current figure. The behavior can be reverted using below command:

hold off

A new figure window can be created using a figure command:

figure

Warning plot and related commands, always use the most recently active figure window.

Other commands useful during plotting:

Final assignment πŸ”₯ πŸ”¨

  1. In a script, create a time vector t = [0:0.01:1]. Generate values of sine functions of two frequencies: 2 Hz i 10 Hz, save them in separate variables, and plot. Specify the color lines to green and red, respectively. Add plot title, axis labels, legend, and grid. Set y axis range to -1.2 to 1.2.
sinus

  1. Calculate a new vector - sum of previously calculated sinusoidal components. Plot it in the same figure, in blue. Change y axis range to -2.5 to 2.5.

  2. Calculate RMS - root mean square value of the result from previous task. Hint You can use mean() to calculate mean value of a vector. Note that elements have to be squared.

rms

Homework πŸ’₯ 🏠

Task 1

A vector x with values [-10:0.01:10] is given. Calculate values of functions described by below polynomials:

poly_1
poly_2

Plot both functions in a figure. Find minimal, maximal and mean values of the function, display them in console (Hint: check mean(), min(), max()).

Task 2

Find out how to place more than one chart in a single figure. Start with built-in help:

doc subplot

Create a figure with two plots one below another. Similarly to Tasks 1 and 2 from Final assignment, plot two sine functions (2 Hz i 10 Hz) on the top plot, and their sum on the bottom plot.

Authors: RafaΕ‚ KabaciΕ„ski, Tomasz MaΕ„kowski, Jakub TomczyΕ„ski